# 探索Circle STARKs近年来,STARKs协议设计趋势是转向使用较小的字段。最早期的STARKs实现使用256位字段,但这种设计效率较低。为解决这个问题,STARKs开始使用更小的字段,如Goldilocks、Mersenne31和BabyBear。这种转变显著提升了证明速度。例如,Starkware能在M3笔记本上每秒证明620,000个Poseidon2哈希值。这意味着只要信任Poseidon2作为哈希函数,就可以解决高效ZK-EVM的难题。本文将探讨这些技术的工作原理,特别关注Circle STARKs这种与Mersenne31字段兼容的方案。## 使用小字段的常见问题在创建基于哈希的证明时,一个重要技巧是通过多项式在随机点的评估来间接验证多项式性质。这大大简化了证明过程。为防止攻击,我们需要在攻击者提供多项式后再选择随机点。在256位字段中这很简单,但在小字段中,可选的随机值太少,容易被攻击者穷举破解。解决方案有两种:1. 进行多次随机检查2. 扩展字段多次随机检查简单有效,但效率较低。扩展字段则类似于复数,可以在有限域上进行更复杂的运算。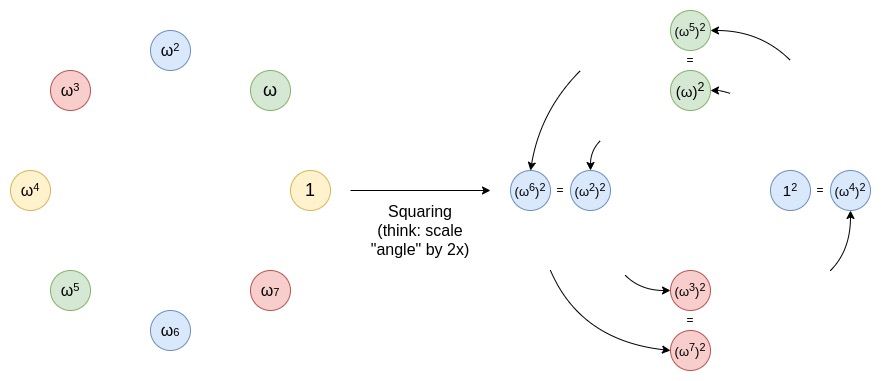## Regular FRI FRI协议的第一步是将计算问题转化为多项式方程。然后证明所提出的多项式解确实满足方程且度数不超过要求。FRI通过将证明多项式度数为d的问题简化为证明度数为d/2的问题来验证。这个过程可以重复多次,每次将问题简化一半。FRI的关键是使用二对一映射将数据集大小减半。这种映射需要能够重复应用,直到最终只剩一个值。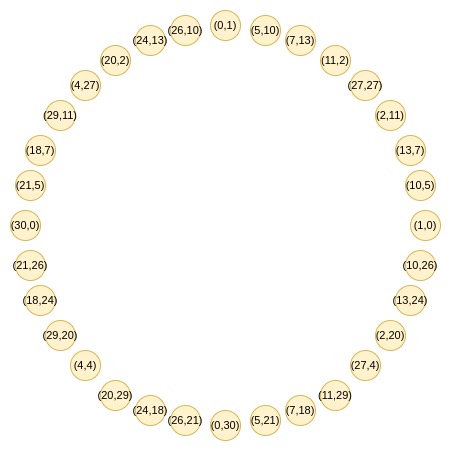## Circle FRICircle STARKs的巧妙之处在于,对于质数p,可以找到大小为p的群,具有类似的二对一特性。这个群由满足特定条件的点组成。这些点遵循一种加法规律,类似于三角函数或复数乘法。从第二轮开始,映射发生变化。每个x代表两个点:(x,y)和(x,-y)。(x → 2x^2 - 1)就是点倍增法则。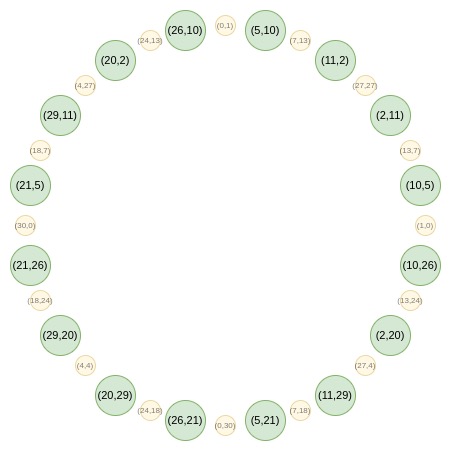## Circle FFTsCircle group也支持FFT,构造方式与FRI类似。但Circle FFT处理的对象不是严格意义上的多项式,而是Riemann-Roch空间。作为开发者,几乎可以忽略这些细节。只需将多项式作为评估值存储,在需要低度扩展时使用FFT。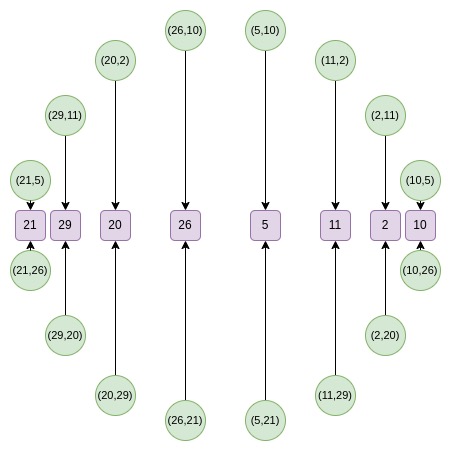## Quotienting在circle group的STARK中,由于没有单点线性函数,需要采用不同技巧替代传统商运算。我们通过在两个点上评估来证明,添加一个虚拟点。## Vanishing polynomials在圆形STARK中,消失多项式为:Z_1(x,y) = yZ_2(x,y) = x Z_{n+1}(x,y) = (2 * Z_n(x,y)^2) - 1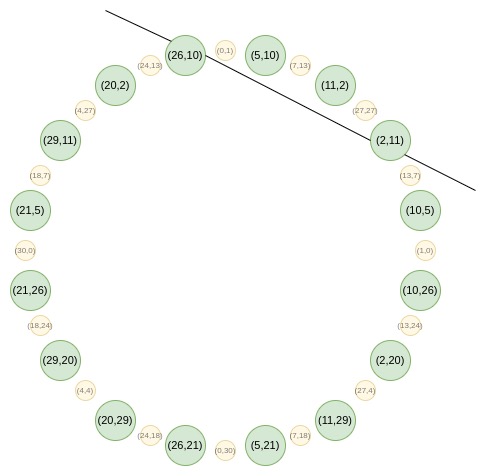## Reverse bit order在STARKs中,多项式评估通常按逆位序排列。Circle STARKs中需要调整这种排序,以反映其特殊的折叠结构。## 效率Circle STARKs非常高效。关键是充分利用计算跟踪中的空间进行有用工作,而不留下大量空闲。与Binius相比,Circle STARKs概念上更简单,但效率稍低。## 结论Circle STARKs对开发者来说并不比常规STARKs复杂。理解Circle FRI和FFTs有助于理解其他特殊FFTs。未来STARK优化可能集中在:1. 最大化哈希函数等基本密码原语的效率2. 递归构造以提高并行化 3. 算术化虚拟机以改善开发体验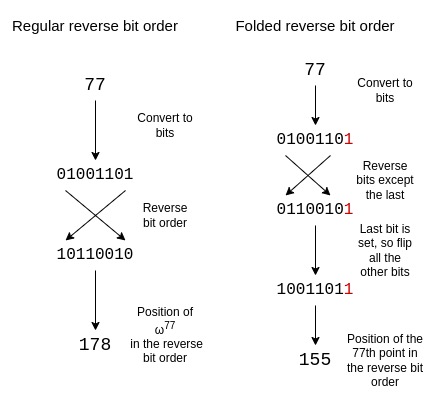
Circle STARKs: 小字段提升ZK证明效率的新方案
探索Circle STARKs
近年来,STARKs协议设计趋势是转向使用较小的字段。最早期的STARKs实现使用256位字段,但这种设计效率较低。为解决这个问题,STARKs开始使用更小的字段,如Goldilocks、Mersenne31和BabyBear。
这种转变显著提升了证明速度。例如,Starkware能在M3笔记本上每秒证明620,000个Poseidon2哈希值。这意味着只要信任Poseidon2作为哈希函数,就可以解决高效ZK-EVM的难题。
本文将探讨这些技术的工作原理,特别关注Circle STARKs这种与Mersenne31字段兼容的方案。
使用小字段的常见问题
在创建基于哈希的证明时,一个重要技巧是通过多项式在随机点的评估来间接验证多项式性质。这大大简化了证明过程。
为防止攻击,我们需要在攻击者提供多项式后再选择随机点。在256位字段中这很简单,但在小字段中,可选的随机值太少,容易被攻击者穷举破解。
解决方案有两种:
多次随机检查简单有效,但效率较低。扩展字段则类似于复数,可以在有限域上进行更复杂的运算。
Regular FRI
FRI协议的第一步是将计算问题转化为多项式方程。然后证明所提出的多项式解确实满足方程且度数不超过要求。
FRI通过将证明多项式度数为d的问题简化为证明度数为d/2的问题来验证。这个过程可以重复多次,每次将问题简化一半。
FRI的关键是使用二对一映射将数据集大小减半。这种映射需要能够重复应用,直到最终只剩一个值。
Circle FRI
Circle STARKs的巧妙之处在于,对于质数p,可以找到大小为p的群,具有类似的二对一特性。这个群由满足特定条件的点组成。
这些点遵循一种加法规律,类似于三角函数或复数乘法。
从第二轮开始,映射发生变化。每个x代表两个点:(x,y)和(x,-y)。(x → 2x^2 - 1)就是点倍增法则。
Circle FFTs
Circle group也支持FFT,构造方式与FRI类似。但Circle FFT处理的对象不是严格意义上的多项式,而是Riemann-Roch空间。
作为开发者,几乎可以忽略这些细节。只需将多项式作为评估值存储,在需要低度扩展时使用FFT。
Quotienting
在circle group的STARK中,由于没有单点线性函数,需要采用不同技巧替代传统商运算。
我们通过在两个点上评估来证明,添加一个虚拟点。
Vanishing polynomials
在圆形STARK中,消失多项式为:
Z_1(x,y) = y Z_2(x,y) = x
Z_{n+1}(x,y) = (2 * Z_n(x,y)^2) - 1
Reverse bit order
在STARKs中,多项式评估通常按逆位序排列。Circle STARKs中需要调整这种排序,以反映其特殊的折叠结构。
效率
Circle STARKs非常高效。关键是充分利用计算跟踪中的空间进行有用工作,而不留下大量空闲。
与Binius相比,Circle STARKs概念上更简单,但效率稍低。
结论
Circle STARKs对开发者来说并不比常规STARKs复杂。理解Circle FRI和FFTs有助于理解其他特殊FFTs。
未来STARK优化可能集中在: